with Guillaume Carlier and Jean-Michel Lasry, Journal of Dynamics and Games, 2021
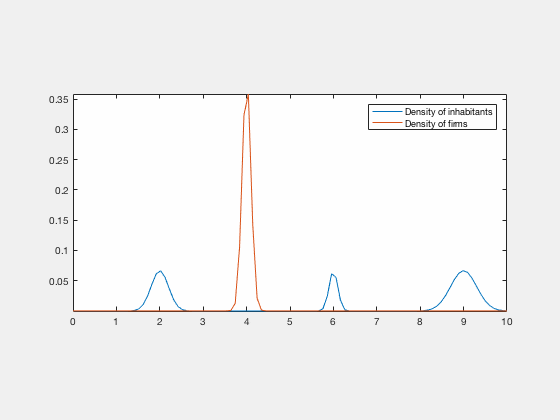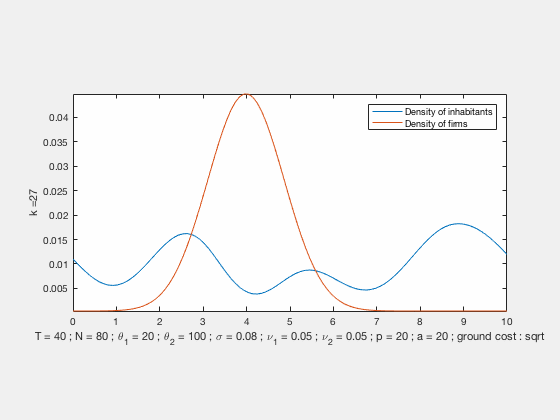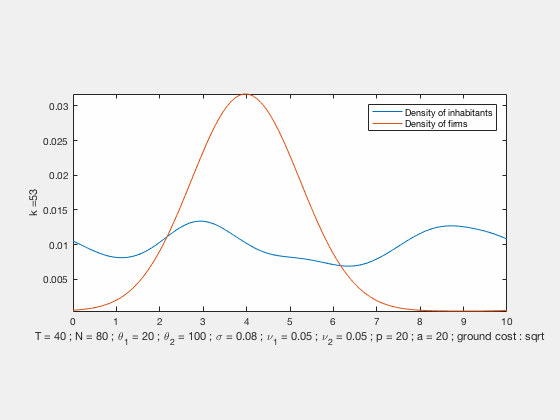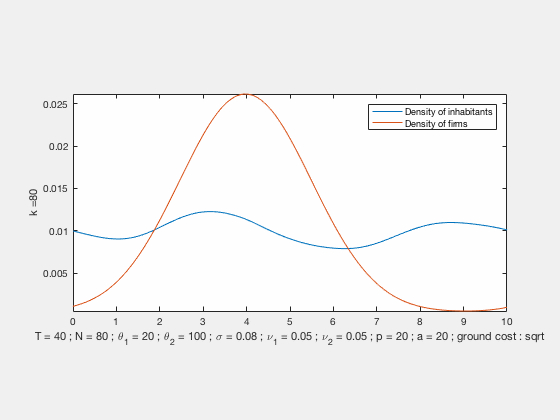
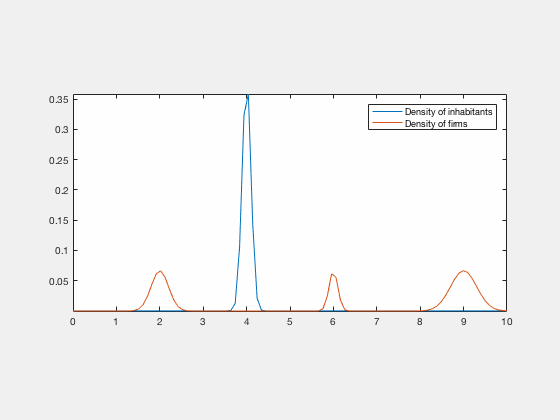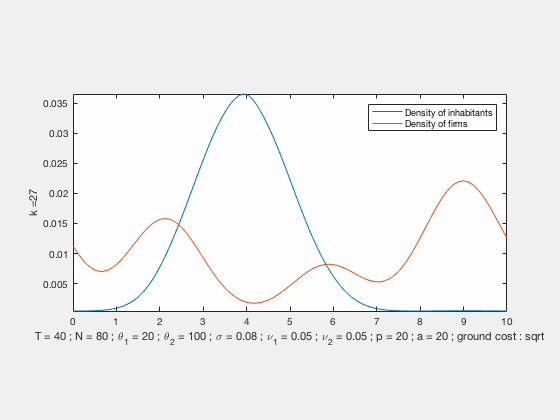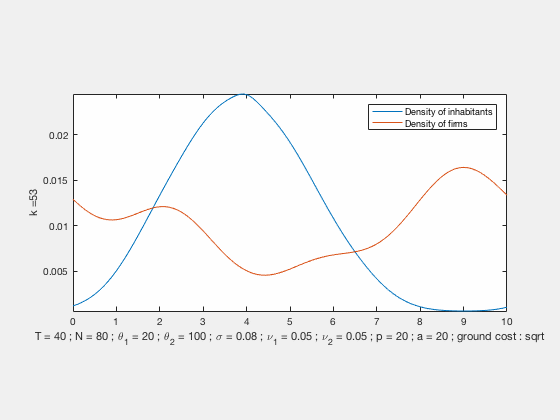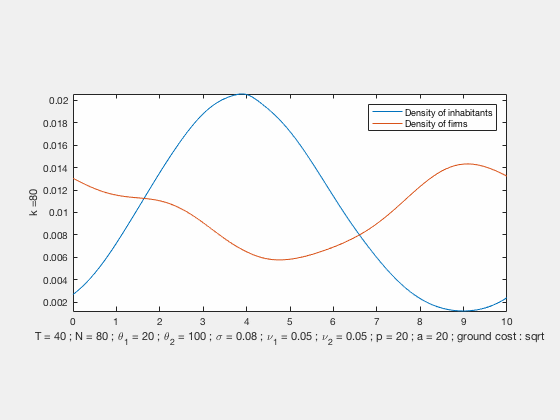
We propose a MFG model for the evolution of residents and firms densities, coupled both by labour market equilibrium conditions at each time and competition for land use (congestion). This results in a system of two Hamilton-Jacobi-Bellman and two Fokker-Planck equations with a new form of coupling related to optimal transport. This MFG has a convex potential which enables us to find weak solutions by a variational approach. In the case of quadratic Hamiltonians, the problem can be reformulated in Lagrangian terms and solved numerically by an IPFP/Sinkhorn-like scheme. We present numerical results based on this approach, these simulations exhibit different behaviours with either residential or business centers depending on the initial conditions and parameters.
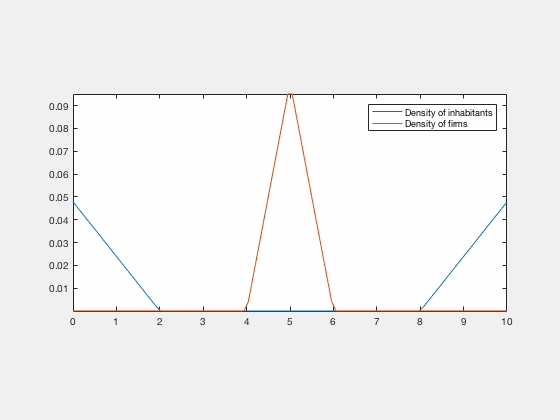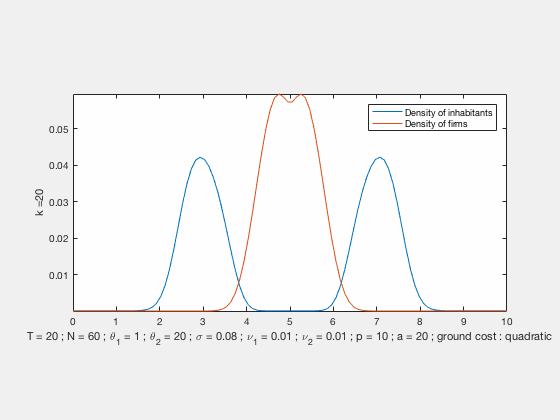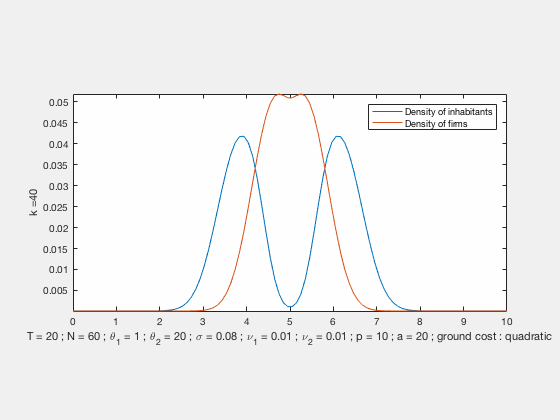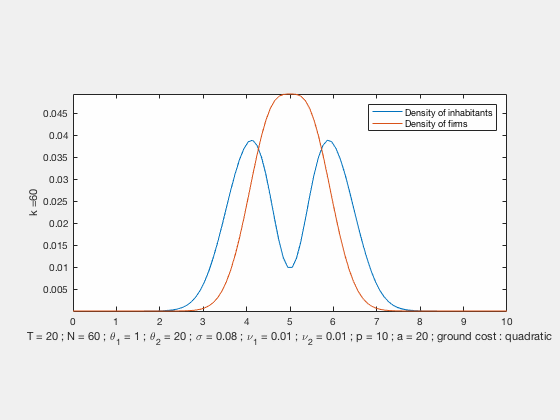
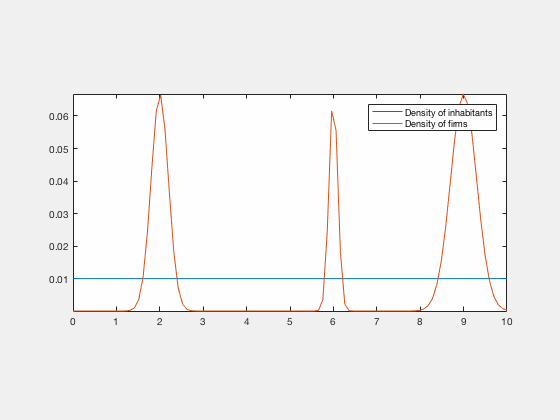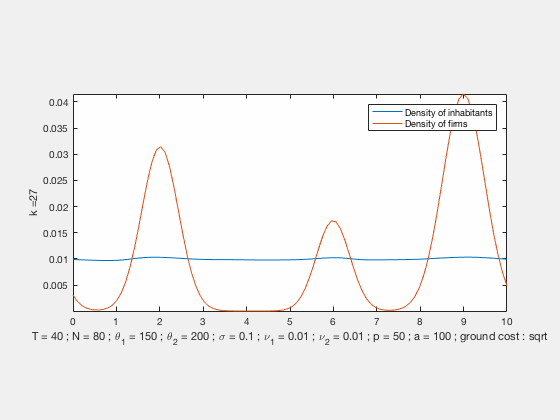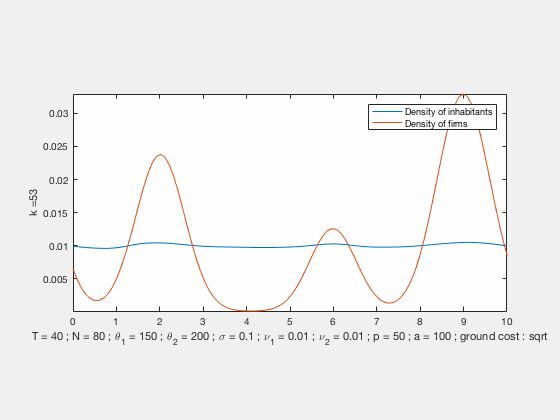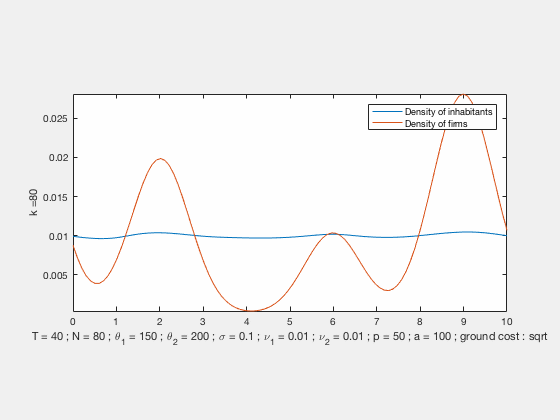
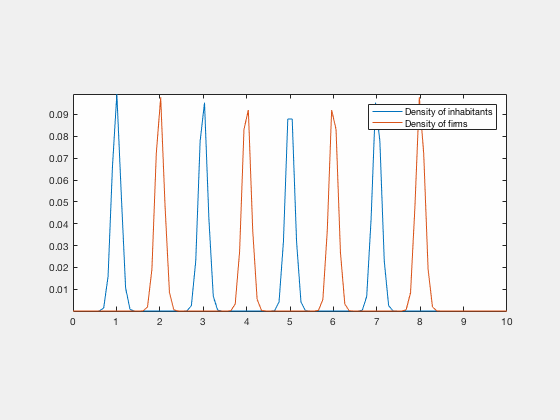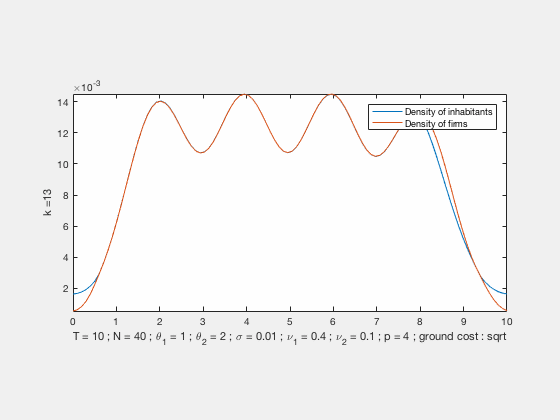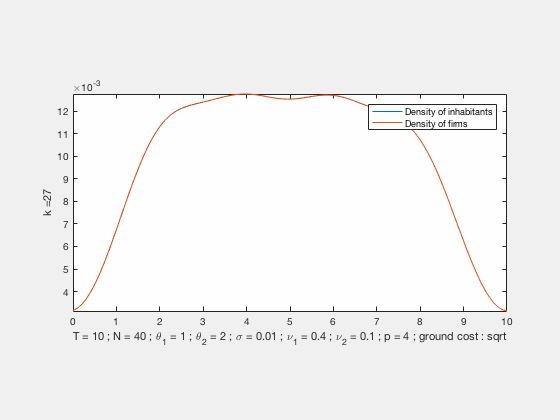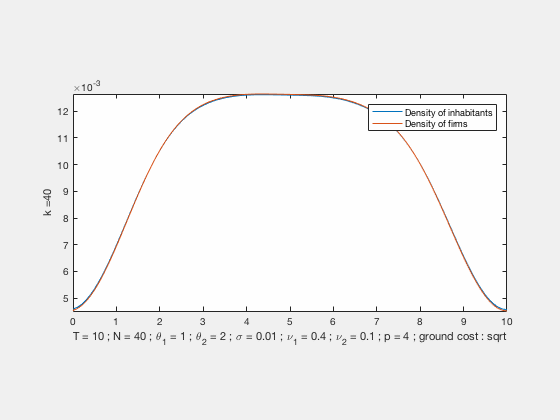
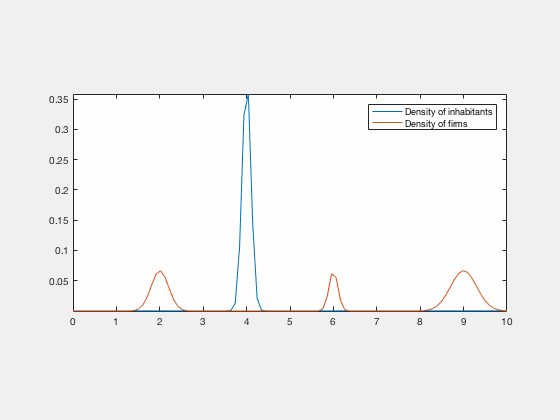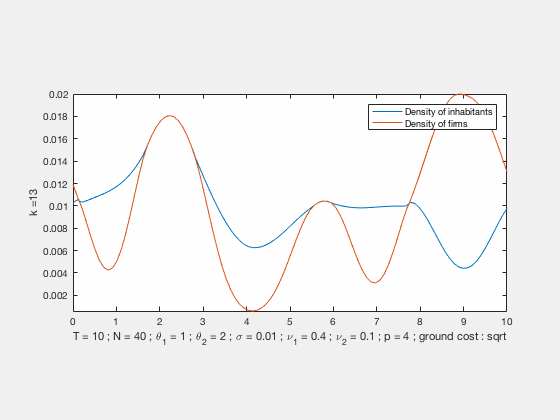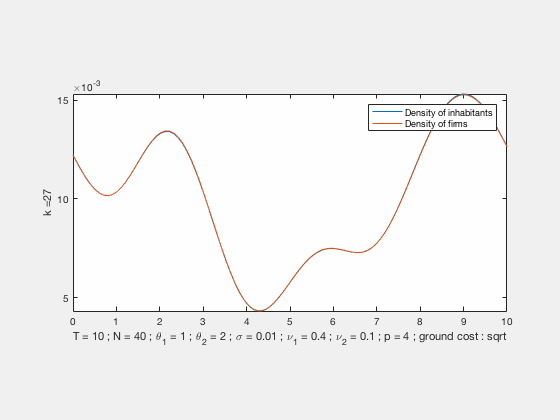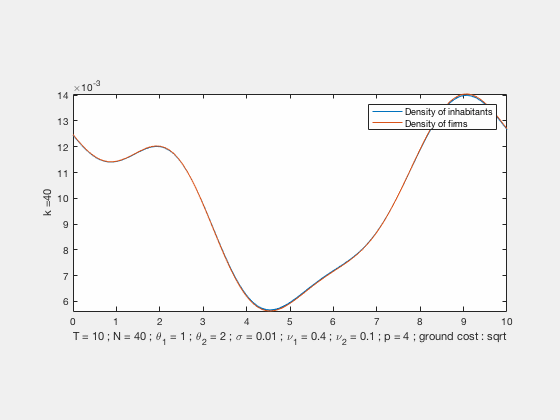
Some examples of simulations :